
Unveiling the Secrets of Force: A Comprehensive Guide to Calculation
Understanding the Fundamental Principles
Imagine trying to move a heavy piece of furniture. That push or pull you feel? That’s force, a fundamental concept in physics. It’s how things interact, how they start moving, stop, or change direction. At its heart, force ($F$) is tied to an object’s mass ($m$) and how quickly it speeds up or slows down, its acceleration ($a$). This relationship is neatly captured by Newton’s second law: $F = ma$. It’s a simple equation, but it explains a lot about how the world works.
Think about pushing a shopping cart. A full cart, heavy with groceries, needs a stronger push to get moving than an empty one. That’s mass at work. Apply the same push to both, and the empty cart will speed up much faster. This connection between weight, speed change, and the push is the core of basic movement science. But, there’s more to it than just this one equation; forces come in many forms, each requiring its own way of figuring it out.
To really get a handle on calculating force, you need to understand the units. We measure weight in kilograms (kg), and speed change in meters per second squared (m/s²). When combined, they give us force in Newtons (N). One Newton is the force needed to move a 1 kg object at 1 m/s². It’s like a universal language for measuring pushes and pulls. Keep your units straight, or you might end up with some wild calculations. You don’t want to accidentally calculate a rocket’s power in, say, butter pats.
Also, forces have direction. They’re like arrows, pointing where the push or pull is going. When many forces act on something, you have to add these arrows together, like solving a puzzle. This is where things can get a bit tricky, but we’ll walk through it step by step.
Delving into Newton’s Second Law: $F = ma$
Applying the Equation in Real-World Scenarios
Newton’s second law, $F = ma$, is your go-to formula for many basic force calculations. Picture designing a car’s brakes. If you know the car’s weight and how fast it needs to slow down, you can figure out the braking force required. This principle is used in many areas, from building bridges to predicting how planets move.
However, the real world often throws curveballs. Things like friction, the force that resists movement, need to be factored in. Imagine a box sliding on a rough surface; friction will slow it down, changing the calculation. This is where we use the coefficient of friction, a number that tells us how rough the surfaces are.
Plus, forces can change over time. A rocket’s push, for example, grows as it burns fuel and gets lighter. In these cases, we use calculus to calculate the force at any instant. That’s why scientists sometimes seem to be writing complex poems, when they’re actually just doing complex calculations.
And don’t forget gravity. It’s a force too. The pull of gravity on an object is its weight, calculated as $W = mg$, where $g$ is the gravity’s pull (around 9.8 m/s² on Earth). It’s what keeps us on the ground. It’s also why a feather and a bowling ball fall differently when air gets in the way.
Exploring Other Types of Forces and Their Calculations
Beyond the Basics: Friction, Gravity, and More
Beyond $F = ma$, there are many other forces, each with its own way of calculating. Friction, as we mentioned, is calculated as $F_f = \mu N$, where $\mu$ is the friction coefficient and $N$ is the normal force. The normal force is the push of a surface against an object.
Gravity, the attraction between objects, is calculated using Newton’s law of universal gravitation: $F_g = G(m_1m_2/r^2)$, where $G$ is a constant, $m_1$ and $m_2$ are the object weights, and $r$ is the distance between them. This is what keeps planets in orbit and apples falling. It’s also why you feel lighter on the moon.
Elastic forces, like those from springs, are calculated with Hooke’s law: $F_s = -kx$, where $k$ is the spring constant and $x$ is the stretch or compression. This is what makes trampolines bounce and rubber bands snap. The minus sign means the force pushes back.
Centripetal force, the force that keeps things moving in a circle, is $F_c = mv^2/r$, where $m$ is the object’s weight, $v$ its speed, and $r$ the circle’s radius. This is what keeps a car turning and a satellite orbiting. Without it, you’d fly off a spinning ride.
The Importance of Units and Vector Addition
Ensuring Accuracy in Force Calculations
To get force calculations right, you need to use units consistently and understand how to add vectors. As we said, force has size and direction. So, when you add forces, it’s not just adding numbers; you’re adding arrows. This often means breaking forces into parts and using math to find the total arrow.
For instance, if two forces push at an angle, you’d split them into horizontal and vertical parts. Then, add the parts separately and use the Pythagorean theorem to find the total force. The direction can be found using trigonometry.
Also, the units you use matter a lot. Make sure they’re the same throughout your calculations. Converting units is a key skill. Like changing kilometers per hour to meters per second or pounds to kilograms. This is where a calculator becomes essential.
A small mistake in units or vector addition can throw off your results. It’s like building something with the wrong measurements; it might look good on paper, but it won’t work in real life. Paying attention to these details is vital for accurate force calculations.
Practical Applications and Real-World Examples
From Engineering to Everyday Life
Force calculations are used in many areas, from building and science to daily life. In building, they’re crucial for designing structures that can handle loads, like bridges and buildings. These calculations ensure safety and stability.
In cars, force calculations are used to design brakes, suspensions, and engines. They help make vehicles safe and perform well. Thinking about the forces in a car crash is important for making safer cars.
In sports, force calculations help improve performance and prevent injuries. Athletes and coaches use force data to analyze movements and techniques. For example, the force of a golf swing can be measured and improved. It’s like having a physics expert on your team.
Even in daily life, we deal with forces. Knowing how to calculate them can help us make smart choices. Like knowing the force to lift something heavy to avoid injury. Or calculating wind force to see how an umbrella will behave. So, next time you lift a box, remember, you’re doing physics.
Frequently Asked Questions (FAQ)
Addressing Common Queries About Force Calculation
Q: What is the difference between mass and weight?
A: Mass is how much stuff an object has, measured in kilograms (kg). Weight is the pull of gravity on that object, measured in Newtons (N). Weight is mass times gravity.
Q: How do you calculate the force of friction?
A: Friction force is the friction coefficient times the normal force. The friction coefficient depends on the materials.
Q: Why is vector addition important in force calculations?
A: Because force has direction. Adding forces is like adding arrows, not just numbers. Ignoring this can lead to big errors.
Q: Can force be negative?
A: Yes. A negative sign usually means the force is in the opposite direction. Like a braking force slowing a car.

How To Calculate Force 6 Steps (with Pictures) Wikihow
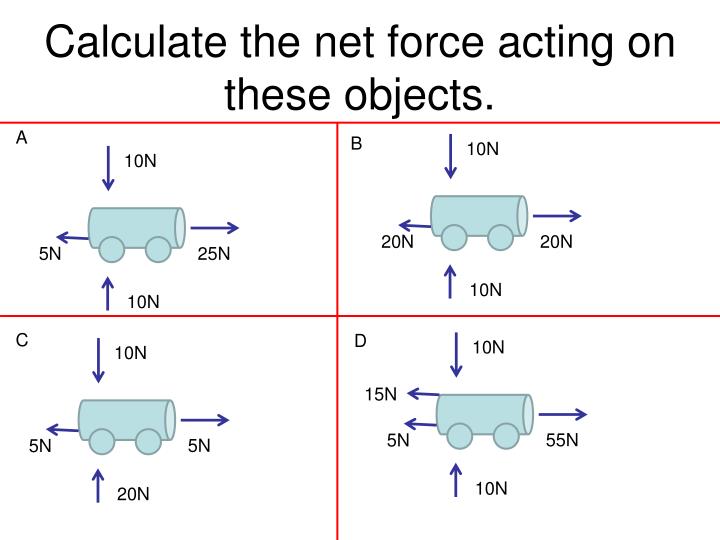
Explain How To Calculate Net Force

How To Calculate Force 6 Steps (with Pictures) Wikihow

How Do I Calculate Force?? R/igcse

How To Calculate The Net Force
